Esta entrada, que inaugura o blog, está dedicada a presentar un traballo de divulgación realizado en colaboración cos meus compañeiros do Departamento de Matemáticas da Universidade de Vigo, José Nicanor Alonso Álvarez e Carmen Quinteiro Sandomingo. Trátase da primeira tradución ao galego das cartas privadas que intercambiaron Pierre de Fermat e Blaise Pascal, dous dos principais matemáticos da primeira metade do século XVII, e que constitúen un fito histórico no desenvolvemento da teoría da probabilidade. A tradución comentada, acaba de ser publicada polo Servizo de Publicacións da Universidade de Vigo.

A tradución fíxose utilizando como texto fonte a edición de 1894 das Oeuvres de Fermat de Paul Tannery e Charles Henry. Un breve resumo do contido do libro apareceu no Boletín da SGAPEIO Informest baixo o título Probabilidade á carta: a correspondencia entre Fermat e Pascal. Esta entrada está basada na ponencia A correspondencia entre Pierre de Fermat e Blaise Pascal que presentamos no XVI Congreso Galego de Estatística e Investigación de Operacións celebrado en A Coruña en outubro de 2023.
Para facerse unha idea inicial da importancia histórica desta correspondencia, recordaréi dúas citas.
Xa fai tempo que se determinaron, nos xogos mais simples, as proporcións entre as posibilidades favorables ou contrarias aos xogadores, e se regularon conforme tales proporcións as apostas e os pagos. Pero ninguén antes de Pascal e Fermat estableceu principios nin métodos para abordar este problema co cálculo […] \’E, pois, a estes dous grandes xeómetras aos que temos que atribuír os primeiros elementos da ciencia das probabilidades, un descubrimento que está á altura dos feitos destacados que fan glorioso o século XVII, o século que máis honra ten proporcionado ao espírito humano.
Pierre Simon Laplace. Essai philosophique sur les probabilités. (1814)
Teñamos en conta que, na época dos nosos protagonistas, as palabras Xeometría e Matemáticas eran sinónimas. Así pois, en opinión de Laplace, o traballo de Fermat e Pascal relativo ao cálculo de probabilidades pode equipararse, por exemplo, ao nacemento do cálculo diferencial, que tamén tivo lugar no séculoXVII. A segunda cita é mais recente:
Cando o meu editor me suxeriu a idea de escribir un libro dedicado a un único documento matemático que tivera cambiado o curso da historia, o meu primeiro pensamento foi a carta que Pascal lle escribiu a Fermat no século dezasete que estableceu a moderna teoría da probabilidade. […] Pouca xente, incluído eu mesmo, leu o orixinal ou se interesou pola súa historia.[…] O que descubrín deixoume maravillado.[…] Unha boa parte do estilo de vida que levamos hoxe é posible grazas ás ideas matemáticas expresadas nesas poucas páxinas.
Keith Devlin. The unfinished game. Pascal, Fermat, and the seventeenth letter that made the world modern. (2008)
Nos compartimos a opinión de Keith Devlin. As circunstancias, o contido e os protagonistas deste intercambio epistolar compoñen un fascinate episodio que merece ser coñecido. E tal é o obxectivo do noso libro, que resumiremos a continuación. Empecemos, xa que logo, falando brevemente dos remitentes das cartas.
Os remitentes
Non nos extenderemos demasiado en evocar as figuras de Fermat e Pascal, xa que son personaxes dabondo coñecidos.
Pierre de Fermat era xurista de profesión e matemático por afección. Mantiña comunicación fluida co abade Marín Mersenne que capitaneaba unha sorte de grupo de eruditos, que se reunían frecuentemente en París, para discutir as novidades científicas do momento: a chamada academia de Mersenne.
A labor de Mersenne foi continuada por personaxes da talla de Pierre de Carcaví ou Jacques Le Pailleur.
Co paso do tempo, estas reunións adquiriron un tono mais formal ata dar lugar a Academia de Ciencias de Francia, fundada en 1666.
Fermat, que apenas deixou traballos escritos, compartía as súas achegas mediante cartas dirixidas aos seus colegas sen proporcionar demostracións e dando moi poucas indicacións dos seus métodos de traballo. O exemplo mais extremo é o da famosa historia do chamado último teorema de Fermat. Descubriu a espiral que leva o seu nome e aplicou o método de descenso infinito.


Blaise Pascal foi un neno prodixio das matemáticas. Dende moi novo asistía co seu pai, Etienne, as reunións do grupo de Mersenne. De saúde moi feble morreu novo, aos 39 anos, deixando un destacado legado científico e filosófico: o triángulo de Pascal, o principio de Pascal, ou a pascalina (unha das primeiras calculadoras mecánicas). A finais de 1654, despois de salir ileso dun accidente tivo unha experiencia relixiosa e decidiu dedicarse á vida contemplativa. Abraza a herexía xansenista, un movemento puritano relixioso, e é entón cando escribe a maior parte da súa obra filosófica. Nesta destacan Lettres provinciales e Pensées, onde expón a chamada aposta de Pascal sobre a existencia de Deus.
O contexto da correspondencia
A afección polos xogos de azar e as apostas formou parte de todas as culturas en todas as épocas. Os xogos de azar eran populares entre os exipcios, babilonios e romanos e distintas formas de entender o azar maniféstanse nas relixións, leis, crenzas, instrumentos económicos, etc. Sorprendentemente, a idea de cuantificar o azar é totalmente allea á ciencia ata o século XVI. Os primeiros intentos, debidos a pioneiros como Pacioli, Tartaglia, ou Galileo, son simples análises de xogos de dados e cartas. E tamén Cardano, que era un xogador empedernido, polo que a súa investigación era con ánimo de lucro.

Xa iniciado o século XVII, outro xogador e apostante case profesional, Antoine Gombaud, que se facía chamar a sí mesmo o cabaleiro de Méré, formuloulle a Pascal dous problemas que o intrigaban. O primeiro, que denominaremos o problema da aposta vantaxosa dicía: «Cantas veces debemos lanzar dous dados para ter vantaxe se apostamos que obteremos polo menos un dobre seis?«. O outro problema, que chamaremos o problema do repartimento era mais complexo:
«Dous xogadores lanzan unha moeda, apostando un deles por cara e o outro por cruz. Ganará aquel que acade primeiro tres acertos. Cando un deles leva ganadas dúas partidas e o outro unha, deben dar por rematado o xogo. Tendo en conta o resultado das partidas xogadas, como deben distribuír os cartos para que o repartimento sexa xusto?«
Varios matemáticos, desde que Pacioli formulara este problema facía xa 150 anos, propuxeron diferentes solucións que non eran satisfatorias. Pascal acepta o reto do cabaleiro de Méré e traballa nos dous problemas. Seguramente, aconsellado por Pierre de Carcaví, decidíu consultar e compartir os seus avances co mellor matemático do momento, Fermat. O resultado é un intercambio epistolar entre os dous sabios no que, entre outras cuestións, sentan as bases do que hoxe chamamos o cálculo de probabilidades.
As cartas
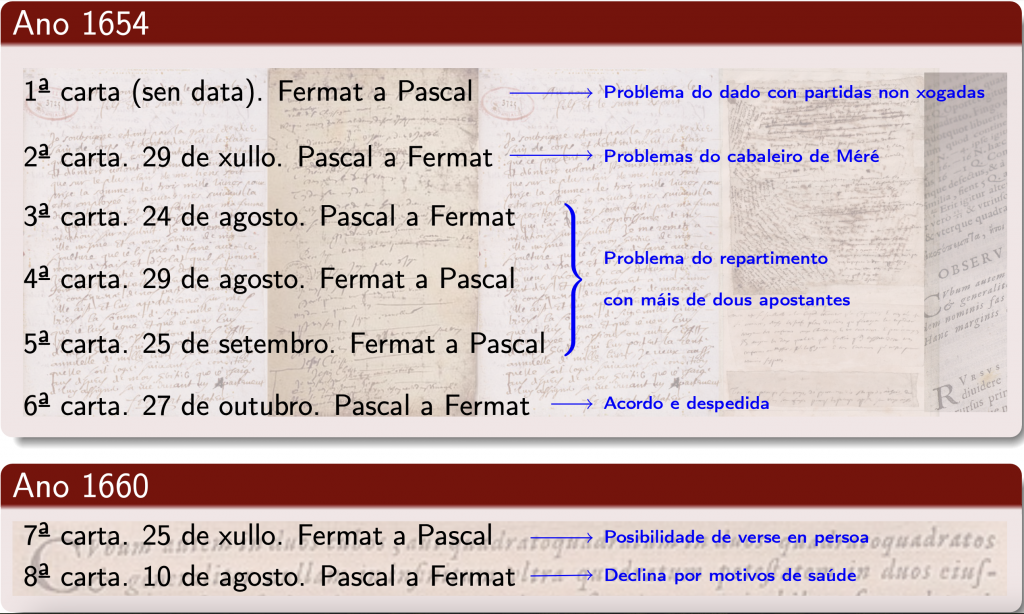
Non todas as cartas que se remitiron Fermat e Pascal chegaron ata nós. Sábese que polo menos se perderon catro, entre elas a que iniciou o contacto. Consérvanse oito. As seis primeiras escribíronse en 1654 e nelas os dous sabios discuten diversas cuestións xeométricas e matemáticas de interese (con un par de demostracións escritas en latín), entre as que destacan os problemas do cabaleiro de Méré. Compre salientar que non se sabe a data en que foi enviada unha das cartas, que os editores modernos colocan na primeira posición da serie. Foi impresa por vez primeira na edición de 1779 das Oeuvres de Pascal, e o editor situouna entre as cartas quinta e sexta da nosa serie. Nela, Fermat discute o problema do dado con partidas non xogadas: «Un xogador aposta contra outro que sacará un seis en oito lanzamentos dun dado. Cal sería a indemnización xusta que debería recibir por renunciar ás catro primeiras tiradas?» Obviamente, este problema está moi relacionado co problema do repartimento.
Cómpre salientar que, dous meses despois deste primeiro intercambio epistolar, Pascal deixou de lado as Matemáticas para dedicarse ás súas reflexións místicas.
Hai, ademais, dúas cartas breves datadas en 1660 que non teñen contido matemático. Fermat escríbelle a Pascal propoñéndolle un encontro. Pascal declina o ofrecemento por motivos de saúde. Os dous sabios non chegaron nunca a coñecerse persoalmente.
Os cálculos probabilísticos da correspondencia
Centrémonos tan só na parte da correspondencia relacionada cos xogos de azar.
Na primeira carta, Fermat resolve o problema do dado con partidas non xogadas. Razoa que a retribución debe ser proporcional ás posibilidades de que o primeiro xogador gane nalgún dos catro primeiros lanzamentos. Obtén a seguinte secuencia, coas probabilidades de ganar no primeiro, segundo, terceiro ou cuarto lanzamentos:

Polo tanto, a resposta é
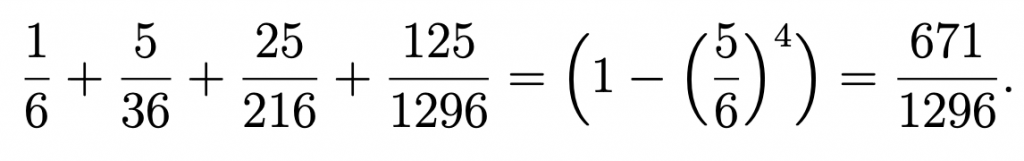
Fermat aclara que se a pregunta formulada fose: «Se aínda non sacou o seis despois de tres tiradas, que indemnización xusta debe recibir por renunciar ao cuarto lanzamento?«, entón a resposta correcta sería 1/6.
Na segunda carta, Pascal aborda os dous problemas propostos polo cabaleiro de Méré. En canto ao problema da aposta vantaxosa, sendo un home observador, o cabaleiro de Méré sabía que, no caso de lanzar un único dado para obter un seis, apostaría con vantaxe de permitírselle catro intentos, nunha proporción de 671 contra 625. Argumentaba que, de lanzar dous dados, como o número de resultados posibles é de 36, para manter a proporción debía realizar 24 tiradas (pois 4 é a 6 como 24 a 36).
Pero pola propia experiencia en infinidade de partidas comprobara que para realizar a aposta con vantaxe debía dispoñer de 25 oportunidades. Entendía que aquela discrepancia entre teoría e práctica indicaba que existía un fallo na Aritmética. Pascal despacha o asunto sentenciando que Monsieur de Méré:
«Ten moi boa mente, pero non é xeómetra, o que é, como vostede sabe, un gran defecto».
Moito máis interese prestaron os nosos protagonistas ao problema do repartimento. Na segunda carta da serie, Pascal felicítase por chegar á mesma solución que Fermat aínda que por camiños distintos: o método das combinación de Fermat e o seu método universal. Pascal describe sucintamente a idea de Fermat que consiste en estender «ficticiamente» o xogo ata o número máximo de partidas posibles, enumerar todos os casos futuros (equiprobables) e contar os que benefician a cada apostante. No caso concreto da situación proposta polo cabaleiro de Méré, quedarían por xogar, como máximo, dúas partidas. Se os xogadores acordaran xogar ambas, aínda que a acadase o terceiro punto no primeiro lanzamento, a ganaría en 3 dos catro posibles resultados. Polo tanto, o repartimento xusto é segundo Fermat 3/4 e 1/4.

Pola contra, o método universal de Pascal, que describe con moito detalle na carta, é un proceso recursivo.
Sexa G(p1,p2) a porcentaxe da aposta total que recibirá o xogador que vai ganando se o xogo se interrompe cunha puntuación p1 e p2. Certamente, nalgunhas situacións simples, o repartimento é claro. Por exemplo, se o primeiro xa ten os 3 puntos entón gana toda a aposta, G(3,p)=1 para p=0,1,2. Se van empatados, reparten a aposta á metade, é dicir, G(p,p)=1/2 para p=0,1,2. Pero entón, podemos calcular o valor G(2,1), xa que hai as mesmas posibilidades de que na seguinte tirada gane a, é entón estamos na situación G(3,1), ou de que gane b, é dicir, empate a dous puntos, G(2,2).
G(2,1)= 1/2G(3,1)+1/2G(2,2)=1/2+1/4=3/4.
Unha vez calculado G(2,1) procedemos dun xeito similar para calcular G(2,0), xa que:
G(2,0)= 1/2G(3,0)+1/2G(2,1)=1/2+3/8=7/8.
E finalmente, calculamos G(1,0), pois
G(1,0)= 1/2G(2,0)+1/2G(2,1)=7/16+1/4=11/16.
Parece claro que Pascal está utilizando, aínda que sexa implícitamente, o concepto de esperanza matemática.
Ata a correspondencia entre Fermat e Pascal non se entendeu ben o concepto de esperanza.
Jan Hacking. The emergence of probability. (1975)
Pascal indica que o seu método pode extenderse a calquera número de partidas. Define o valor da partida i como V1=G(1,0)-1/2 e Vi=G(i,0)-G(i-1,0) se i=2,3. Presenta varias fórmulas, sen demostración, para o caso particular de 8 partidas. Por exemplo, á pregunta: «Sendo dado o número de partidas que se queira, atopar o valor da primeira», responde coa expresión:
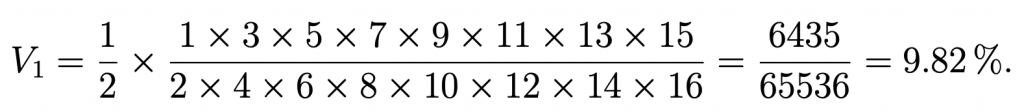
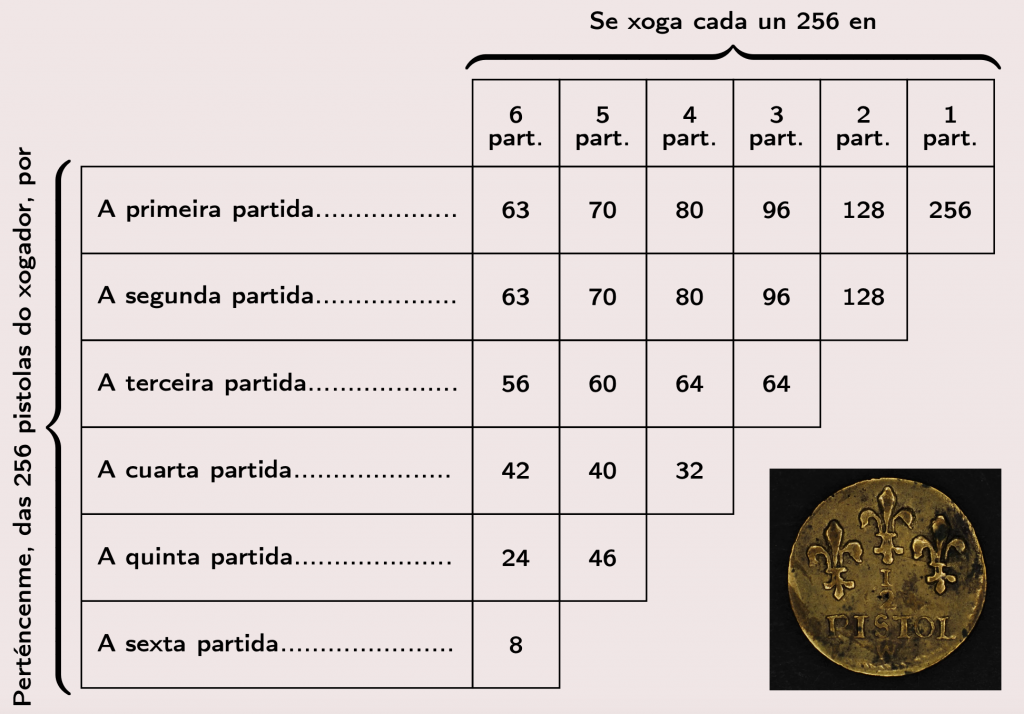
Completa unha táboa cos todos os valores das partidas para o caso dun xogo a 6 puntos no que se apostan 256 pistolas (a pistola era unha moeda da época, tamén chamada louis de ouro, polo rei Louis XIII de Francia que aparecía no anverso, equivalente a dez libras francesas).
Na terceira, cuarta e quinta cartas Pascal e Fermat discuten o problema do repartimento cando hai máis de dous xogadores. Pascal mantivo informados aos seus colegas da academia de Mersenne da súa comunicación con Fermat. Un deles, Gilles de Roberval, poñía reparos ao método das combinacións, xa que non tiña claro que o xogo real e o das «partidas ficticias» fosen sempre equivalentes.
Con dous xogadores, Pascal non vé reparo ningún. Se supoñemos, por exemplo, que ao xogador a lle faltan 2 puntos e ao b tres, entón o xogo resolveríase como moito en 4 partidas. Nas 16 combinacións posibles o ganador do xogo real e o das partidas ficticias é o mesmo (Nas táboas os resultados das partidas van en columna, e na última fila indícase o xogador que gana).
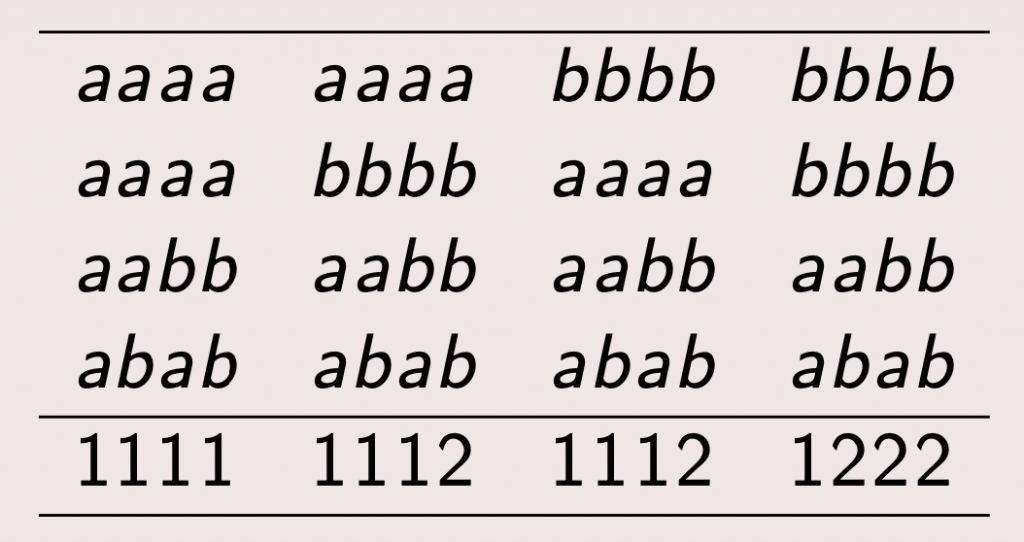
Pero no caso de tres xogadores a cousa non estaba tan clara. Supoñamos que o xogo se interrompe cando a un deles lle falta un punto para ganar e aos outros dous puntos. Agora temos 27 combinacións dadas polos distintos resultados equiprobables nas 3 partidas que, como moito, se poderían chegar a disputar.
Fermat propón o reparto (17,5,5). Pascal asegura ter chegado a ese mesmo reparto utilizando o seu método recurrente.

Pero agora súmase as dúbidas de Roberval e non ten claro que a situación ficticia e a real sexan equivalentes. Pensemos na combinación particular marcada en cor azul na táboa:
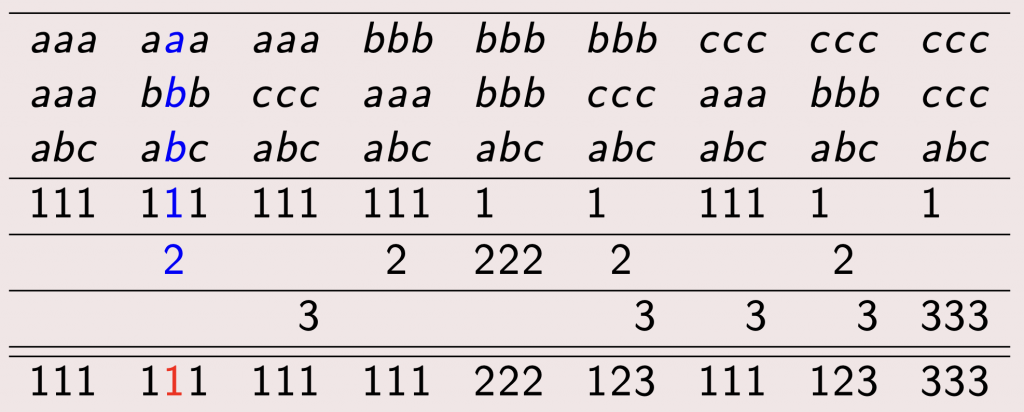
Aquí, os xogadores a e b rematarían os dous cos mesmos puntos é, daquela, deberían repartir a ganancia a partes iguais. En total temos 14 combinacións hipotéticas nas que o resultado final sería de «empate» entre dous xogadores (que se indican nas filas intermedias, na última fila segue figurando o ganador de acordo co razoamento de Fermat). Tendo en conta os empates o reparto xusto sería (16,5+1/2,5+1/2). Fermat responde explicando que a orde en que se ganan as partidas é relevante á hora de contar os casos favorables. Para eliminar calquera tipo de dúbida expón un brillante razoamento alternativo que evita as «partidas ficticias».
Na última carta do ano 1654, Pascal acepta as explicacións de Fermat e dá por concluido o intercambio. Qué aconteceu despois?
Consecuencias da correspondencia
No ano 1654, Pascal estaba redactando o seu Traité du triangle arithmétique (Tratado do triángulo aritmético), que se publicou como obra póstuma en 1665. Probablemente, trala correspondencia con Fermat, engadiu no capítulo final Divers usages du triangle arithmétique un novo apéndice titulado Usage du triangle arithmétique pour déterminer les parties qu’on doit faire entre deux joueurs qui jouent en plusieurs partie, dedicado ao problema do repartimento, no que demostra formalmente o seu método universal.

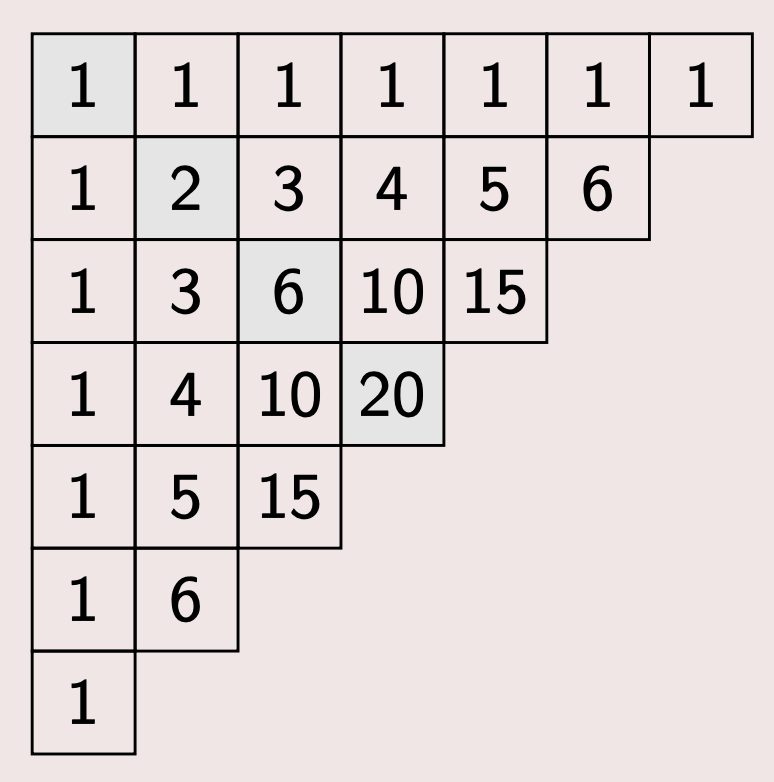
O propio Pascal era consciente de que as cuestións que tratara con Fermat eran o xerme dunha novedosa teoría. Él mesmo escribíu nun artigo dirixido á Academia de París en 1654:
Ao unir así as demostracións das Matemáticas á incerteza do azar, e ao conciliar o que parece contrario, tomando o seu nome das dúas, esta arte arrógase con todo dereito este título asombroso: a Xeometría do azar
Co tempo, o grupo orixinal de Mersenne foi crecendo ata dar lugar, en 1665, á fundación da Academia de Ciencias de Francia. Esta pintura mostra o acto de presentación dos académicos ao rei Luis XIV. Ahí están, por exemplo, Pierre de Carcavi, e seguramente Roberval, e un xoven e talentoso científico holandés, Christian Huygens, que se unira ao grupo na súa visita a París en 1655.

Huygens escribiu o primeiro libro sobre probabilidade da historia De ratiociniis in aleae ludo en 1658. No limiar explica que:
É necesario saber, por outra parte, que xa hai un tempo que algúns dos mais célebres matemáticos de toda Francia se ocuparon deste tipo de cálculo, para que ninguén me atribúa a honra da primeira invención xa que non me pertence.
Durante cincuenta anos o texto de Huygens foi o único tratado sobre probabilidades. A influencia nas seguintes obras, xa clásicas, na historia da probabilidade é innegable. Na parte final do libro formulou cinco problemas como reto para a comunidade matemática. Varios autores estudaron os problemas propostos, achegando solucións e xeneralizacións: Jacob Bernuilli (1654-1705) na súa obra póstuma Arts conjectandi de 1713; Pierre Rémond de Montmort (1678-1719) en Essay d’analyse sur les jeux de hazard de 1708; ou Abraham de Moivre (1667-1754) en De mensura sortis publicado en 1711. O recoñecemento ao traballo pioneiro de Fermat e Pascal é compartido por todos os autores posteriores. Vexamos algúns exemplos significativos:
Un problema relativo a un xogo de azar proposto a un austero xansenista por un home de mundo é a orixe do cálculo de probabilidades.
Simeón Denis Poisson. Recherches sur la probabilité. (1837)
O problema que o cabaleiro de Méré (un xogador empedernido) lle propuxo ao recluido de Port Royal (que todavía non cambiara o interese pola ciencia polas distracións asociadas á contemplación da «grandeza da miseria humana»), foi o primeiro dunha longa serie de problemas que fixeron xurdir novos métodos de análise en matemáticas, e que prestaron un invaluable servizo nos aspectos prácticos da vida.
George Boole. The laws of thought. (1854)
O problema dos puntos discútese na correspondencia entre Pascal e Fermat, e entón a teoría da probabilidade comeza a súa carreira.
Isaac Todhunter. A history of the mathematical theory of probability. (1865)
Temos a certeza de que Pascal foi consciente de que xunto con Fermat sentou as bases dunha nova disciplina que revolucionaría a nosa cosmovisión.
Alfréd Rényi. Cartas sobre probabilidad. (1967)
A nosa tradución é unha modesta achega ao amplo inventario de artigos e libros que analizan este singular episodio da historia da probabilidade. Esperamos que sexa do voso agrado.
Bibliografía
- Alonso Álvarez, J. N., Mirás Calvo, M. \'{A}, e Quinteiro Sandomingo, C. (2023). Probabilidade á carta: a correspondencia entre Fermat e Pascal. Informest, 65:2-5.
- Basulto Santos, J. e Camúñez Ruiz, J. A. (2007). El problema de los dados del caballero de Méré: soluciones publicadas en el siglo XVII. SUMA, 56:43-54.
- Basulto Santos, J. e Camúñez Ruiz, J. A. (2007). La geometría del azar. Editorial Nivola.
- David, F. N. (1962). Games, gods and gambling: a history of probability and statistical ideas. Hafner Publishing Company, New York.
- Devlin, K. (2008). The unfinished game: Pascal, Fermat, and the seventeenth-century
letter that made the world modern. Basic Books. - Diaconis, P. e Skyrms, B. (2018). Ten great ideas about chance. Princeton University Press.
- Gorroochurn, P. (2014). Thirteen correct solutions to the «problem of points» and their
histories. The Mathematical Intelligencer, 36:56-64. - Hacking, I. (1975). The emergence of probability. A philosophical study of early ideas about probability, induction and statistical inference. Cambridge University Press.
- Rényi, A. (2022). Cartas sobre probabilidad. Soutiño Editora.
- Rueda, R. (2018). Blaise Pascal y Pierre de Fermat. ¿Los
fundadores de la probabilidad? Miscelánea Matemática, 65:55-68. - Sandford, V. e Merrington, M. (1998). Fermat and Pascal on probability. https://www.york.ac.uk/depts/maths/histstat/pascal.pdf.
- Tannery, P. e Henry, C., editores (1894). Oeuvres de Fermat. Tome deuxième. Correspondance. Gauthiers-Villars et fils.
- Todhunter, I. (1865). A history of the mathematical theory of probability. From the
time of Pascal to that of Laplace. Macmillan and Co.